Tantalum polymer capacitors are expanding their market share in the commercial world because they offer superior electrical performance (primarily much lower ESR), have outstanding reliability, and display a more benign failure response than the incumbent MnO2-cathode tantalum capacitor technology. It is natural that engineers want to use this new technology in high-reliability applications.
However, a key reliability assessment tool for MnO2-cathode tantalum capacitors – Weibull grading per MIL-PRF55365 – is often ineffective when applied to tantalum polymer capacitors. Because this well-established tool often proves ineffective, a new reliability assessment strategy is needed and has now been developed by KEMET.
The basic principles behind the Weibull grading technique are reviewed, as are the reasons why it is often ineffective when applied to tantalum polymer capacitors. Then a new reliability assessment strategy for tantalum polymer capacitors is described. Special emphasis is placed on differences in the typical time-to-failure responses of tantalum polymer capacitors versus MnO2-cathode tantalum capacitors during this discussion. Finally, an example is given of successful use of this new reliability assessment strategy in a real-world high-reliability application.
In the high-reliability community, it is often difficult to introduce new technologies. While the new technology may provide performance advantages that are very attractive to design engineers, the incumbent technology often retains a bureaucratic advantage that impedes adoption of the new technology.
One specific example of this advantage is that existing reliability testing standards may be highly tuned to the specific characteristics of the old technology and may not fit the new technology very well. Unless the new technology can be made to behave exactly the same way as the old technology, it may not be possible to achieve acceptable results when applying the existing reliability test methods. If the advantages of the new technology are to be enjoyed, these test methods must be modified to accommodate the different characteristics of the new technology while at the same time effectively accomplishing the reliability assessment objectives of the original test methods.
This situation is certainly true for tantalum polymer capacitors when one attempts to perform reliability assessment. Tantalum polymer capacitors offer specific performance advantages over MnO2-cathode tantalum capacitors, but it is often difficult to establish the batch/lot reliability of these capacitors by traditional methods. This is true because the behavior of tantalum polymer capacitors during accelerated life testing is different from that of traditional MnO2-cathode tantalum capacitors.
Some advantages of tantalum polymer capacitors are: (1) much lower ESR, (2) better stability of capacitance and ESR versus temperature, (3) more uniform dielectric robustness that can provide superior reliability, and (4) a more benign failure mechanism that, while still leading to short-circuit failure, avoids the undesired transient thermal event that is possible with many MnO2-cathode tantalum capacitors. One challenge associated with tantalum polymer capacitors is that the traditional reliability assessment tool for MnO2-cathode tantalum capacitors – Weibull grading – often does not produce satisfactory results because too few capacitors fail under the accelerated test conditions to support the associated failure rate calculations.
The purposes of this paper are to describe why the Weibull grading method of MIL-PRF-55365 is often inadequate to assess the reliability of tantalum polymer capacitors, introduce a new reliability assessment test that accomplishes the same objective as Weibull grading, but in a different way, and give an example of customer success that resulted from use of this new reliability assessment technique.
In order to understand why Weibull grading often doesn’t work well with tantalum polymer capacitors, it is useful to review the Weibull grading method itself to allow clear understanding of the mismatch between this test method and the improved failure behavior of tantalum polymer capacitors. The MIL-PRF-55365 Weibull grading method will now be briefly reviewed.
The strategy of the Weibull grading method is that a fairly large sample of capacitors from a single batch is lifetested under accelerated conditions to determine how quickly the rate of early lifetest failures declines. Time-to-failure data are fit to the Weibull statistical distribution and failure rate (FR) calculations are made to determine (1) that the failure rate is indeed declining with time and (2) how long the capacitors must be exposed to the accelerated conditions for the surviving capacitors to reach the desired low failure rate.
Once this information is determined for the sample, the rest of the batch is exposed to the same accelerated conditions for the same time duration that was used for the sample. The capacitors that survive this process are “graded” with the target failure rate (e.g., 0.001%/1000h = Weibull D failure rate).
As with any testing protocol, there are specific detailed steps that support the overall strategy. Weibull grading per MIL-PRF-55365 follows this procedure:
* If no failures occur after 10 hours, use MIL-STD-690 FRSP-90 Table II to find how many accelerated unit hours you need to accumulate with an acceptable number of failures to reach the target FR (e.g., 389 million unit hours with only 1 failure to claim 0.001%/1000h)
Fig. 1 contains graphs and formulas reproduced from the Weibull grading test method described in MIL-PRF-55365H (see http://www.landandmaritime.dla.mil/Downloads/MilSpec/Docs/MIL-PRF-55365/prf55365.pdf). The left half of the figure pertains to the cumulative fraction failed graph that is created using the two fractions failed p1 and p2. The points associated with p1 and p2 are plotted on the graph and a straight line is drawn between the points. The slope of this line is the Weibull β parameter.
The true scaling of this graph appears at the top and on the right hand side. Nonlinear auxiliary scales that are easier to read appear at the bottom and left hand side of the graph. The purpose of the special scaling is to allow all pertinent Weibull distributions to be drawn as straight lines on the graph. If the straight line has slope equal to 1, the failure rate is constant (exponential failure distribution). If the slope is greater than 1, the failure rate is increasing with time and if the slope is less than 1, the failure rate is decreasing with time. A fundamental assumption behind MIL-PRF-55365 Weibull grading is that the failure rate of MnO2-cathode tantalum capacitors decreases in time.
Formulas are provided to define the functional form of the Weibull cumulative fraction failed versus time distribution and provide an algebraic manipulation of this formula that allows calculation of the Weibull β parameter. The origin of the special scaling of the linearized cumulative fraction failed graph can be seen in the formula for the Weibull β parameter.
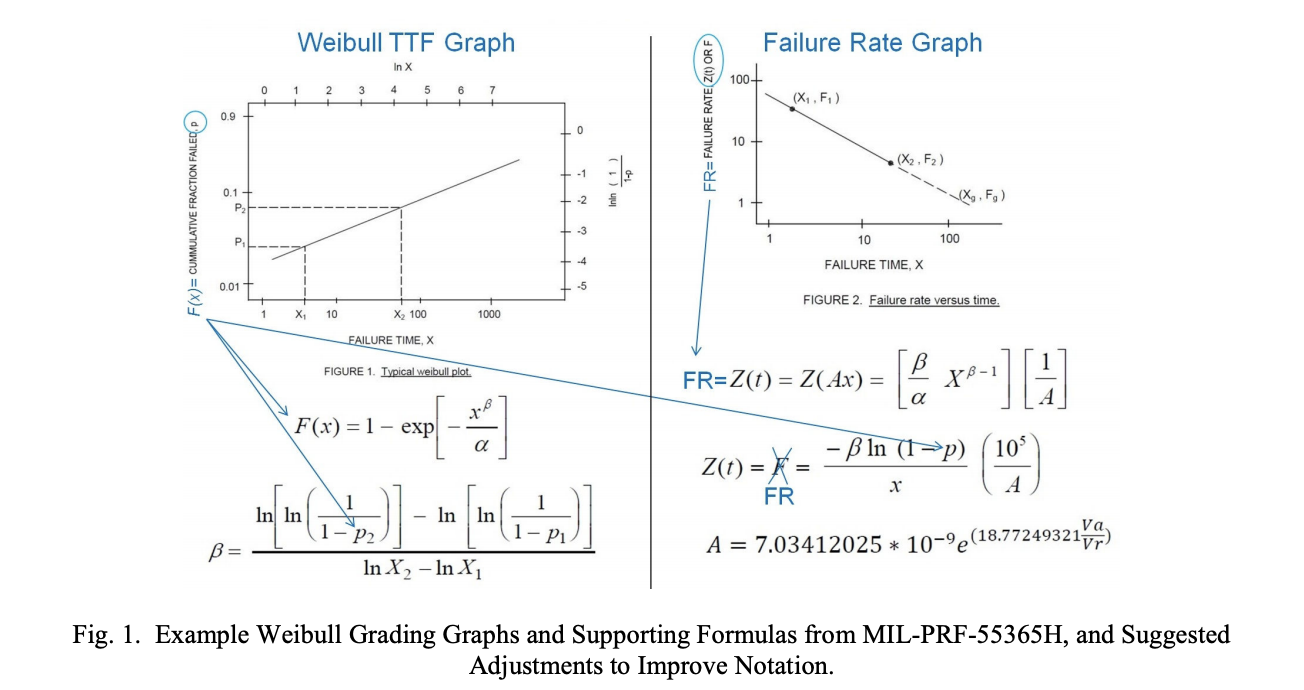
The right half of the Fig. 1 pertains to the calculation and plotting of failure rate versus time-based on the cumulative fraction failed versus time data and the Weibull β parameter. Two formulas are given for failure rate versus time. Finally, an acceleration formula is provided to define how much faster failures should be assumed to occur in time as the test voltage is raised.
The first failure rate formula is derived from the Weibull cumulative fraction failed formula, while the second formula is an algebraic manipulation of the first formula that is more practical to work with. Both formulas take into account the degree of acceleration of the life test. The second formula adds a factor of 10^5 to scale the results from fraction failed per hour to percent per 1000 hours. The second formula also eliminates the need to estimate the Weibull α parameter from the cumulative fraction failed graph.
While the formulas and graphs of Fig. 1 are separately accurate, the consistency of notation is poor. It is highly irregular to use the same symbol “F” to represent both the cumulative fraction failed versus time and the failure rate. It is this author’s opinion that the failure rate formula would be much better identified with the symbol “FR.” Also, nowhere is it explicitly stated that F(x) is the same quantity as p, the cumulative fraction failed.
The blue additions and adjustments to the axis labels and formulas are this author’s suggestions regarding how the notation could be improved with minimal editing. The blue lines and circles are intended to draw the reader’s attention to the clues that allowed the author to decipher the current notation.
An example of some real (but not graphed precisely as described in MIL-PRF-55365) Weibull grading data appears in Fig. 2. The first failure in the cumulative fraction failed versus time graph (top) occurs before 10 hours and the Weibull β parameter can be determined at t = 40 hours. Since β < 1 (β ~ 0.5), the failure rate is falling with time as is required for successful Weibull grading.
The deviation from MIL-PRF-55365 in this graph is that β is calculated from all of the data points (see the black best-fit line), not just p1 at 2.2 hours and p2 at 40 hours per the MIL-PRF-55365 procedure (see the solid violet line). The dashed violet line provides yet another estimate of β. This estimate of β involves drawing a line through the point corresponding to p1 and a second point corresponding to the cumulative fraction failed at 1000 hours. This estimate of β attempts to account for the additional test time that elapsed without failures at the end of this 1000 hour test.
It is interesting to note that real Weibull time-to-failure data rarely fit a straight line. This leaves room for disagreement regarding the “correct” value of β.
In the case of the data in Fig. 2, it is even arguable that a superior estimate of β could be made by fitting a line to only the points that fall between roughly 50 hours and 600 hours where the slope of the line has substantially stabilized at a lower value than is true for the earlier data. There is certainly some useful information lost when one employs the two-point simplification required by the test procedure of MIL-PRF-55365.
The failure rate versus time graph appears below the cumulative fraction failed graph in Fig. 2. There are two lines plotted: (1) the actual failure rate under accelerated conditions (top line) and (2) the projected failure rate at rated voltage based on the voltage acceleration formula in Fig. 1 (bottom line). The bottom line is offset down along the Yaxis from the top line by the voltage acceleration factor A (a factor of 1,824 in this case).
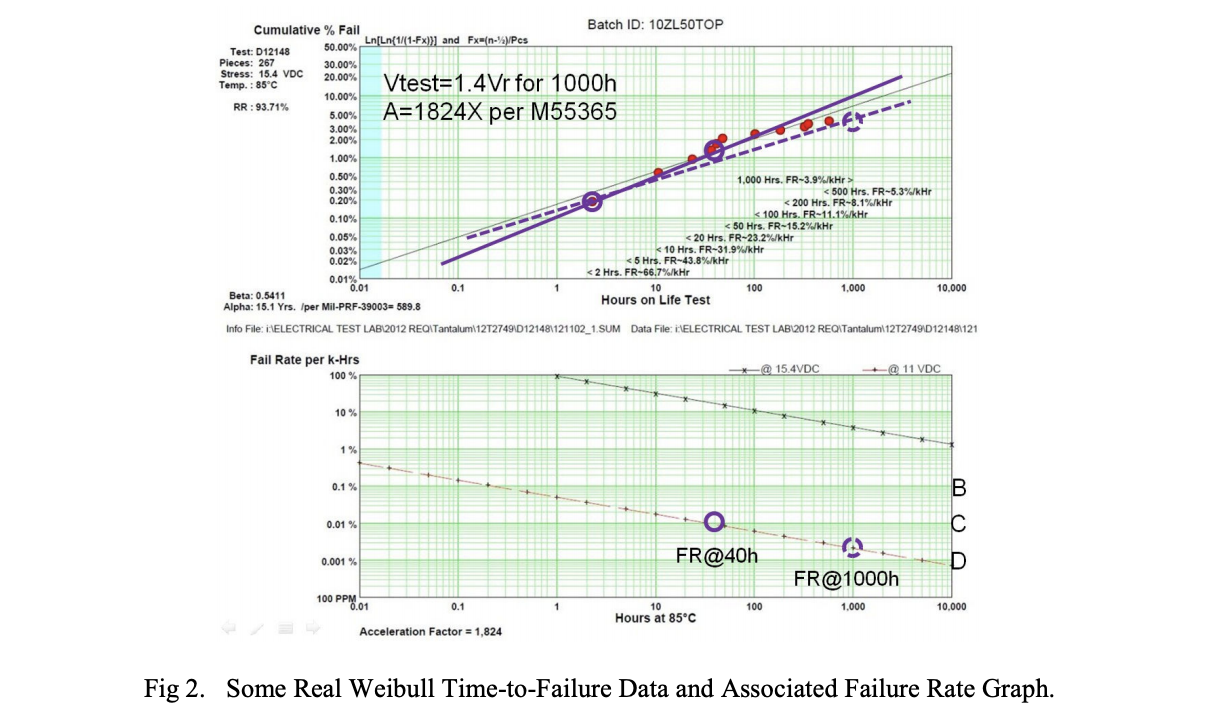
At 40 hours these parts do not quite reach Weibull C failure rate strictly following MIL-PRF-55365, but would do so after only a few more hours of grading. But if it were necessary to reach Weibull D failure rate, the parts would have to be graded for many thousands of hours which is probably not a practical choice since a significant fraction of useful life could be consumed in the grading process and expensive testing resources would be occupied for an extended period of time.
In spite of its imperfections, the MIL-PRF-55365 Weibull grading method has been a good tool to establish the reliability of many MnO2-cathode tantalum capacitor batches. Its chief advantage over its predecessor, the Established Reliability (ER) test methodology, is that it provides a batch-by-batch estimate of reliability instead of a long-term averaged assessment over a relatively few batches (additional details on ER test methodology are provided later). It is only when there are no, or very few, early failures that Weibull grading really shows its limits.
It did not take long to identify a problem when the MIL-PRF-55365 Weibull grading method was first applied to tantalum polymer capacitors. Simply stated, the problem was that no capacitors failed during the first 10 hours of testing, even at the maximum allowed voltage acceleration.
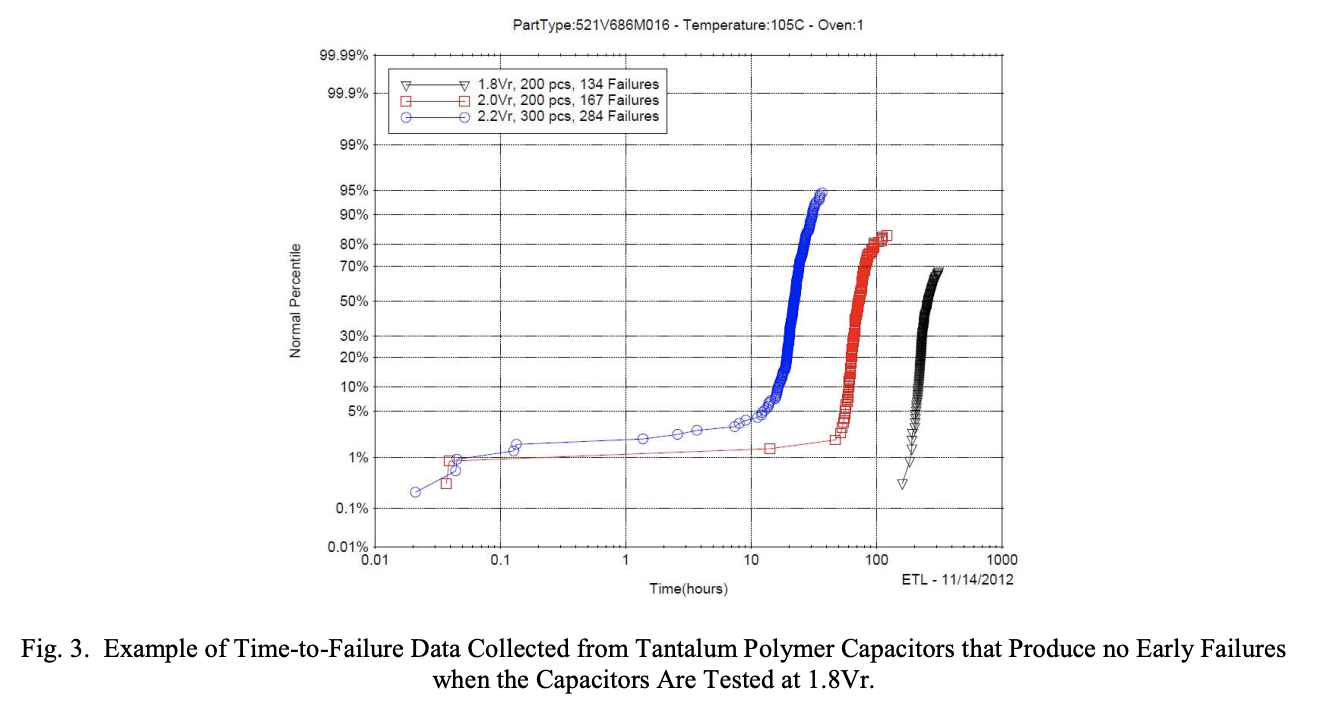
Fig. 3 contains data from a time-to-failure lifetest of some 68uF, 16V tantalum polymer capacitors at 105oC (note that the test temperature is higher than the 85oC required by MIL-PRF-55365). Observe that the curve for testing at 1.8Vr shows that even at this highly accelerated test condition, no early failures occur in the first 10 hours. The same would certainly be true at lower stress conditions, including the maximum allowed MIL-PRF-55365 Weibull test conditions of 1.53Vr at 85oC.
Some early failures start to occur at 2.0Vr. But after one excludes the infant mortals that occur before t = 5 minutes (0.083 hours) according to the MIL-PRF-55365 rules, the first valid failure does not occur until after 10 hours. So the Weibull procedure fails and one is forced to use the FRSP-90 tables to calculate the failure rate.
Note that at these very stressful conditions (2.0Vr), wearout begins at roughly 50 hours. Wearout occurs even earlier when the voltage is raised to 2.2Vr. So even if the rules for Weibull grading were adjusted to allow for use of high enough test voltage to cause valid early failures, there would be a new problem introduced – the grading process would consume an unreasonably large fraction of the useful life of the capacitors, perhaps almost all of it in the case of the 2.2Vr test of Fig. 3.
If one is forced to follow MIL-PRF-55365 as written and no valid failures are observed within the first 10 hours, the only alternative is to calculate the failure rate by applying the FRSP-90 tables. The number of required test hours is very high. To achieve a failure rate of 0.001%/1000h (Weibull D failure rate), 389,000,000 total test hours are required with only 1 failure allowed.
The FRSP-90 tables are associated with the Established Reliability method that preceded Weibull grading for solid tantalum capacitors. Under the ER test method, samples were taken from specifically-identified part numbers for qualification and from representative part numbers currently in production for maintenance of qualification. These samples were lifetested for 10,000 hours at 85oC with rated voltage applied to accumulate the part hours required for the various reliability levels (level S was for 0.001%/1000h which is now called Weibull D).
Under the ER reliability assessment method, not every part number was tested, and certainly not all batches manufactured for a given part number were tested. But because no acceleration was allowed, the process often required years of testing to support qualification of a new design and considerable ongoing testing to maintain that qualification.
At least MIL-PRF-55365 allows the use of voltage acceleration to speed the accumulation of the hundreds of millions of part hours required per FRSP-90. But it does not allow temperature acceleration, so it still takes much more testing to achieve a specific Weibull failure rate under FRSP-90 than it does when there are enough failures to support Weibull grading. Thus, in effect, one is penalized for the misfortune of having parts that do not fail.
Some other concerns with both Weibull grading and the FRSP-90 alternative under MIL-PRF-55365 are: (1) the voltage acceleration factor given in MIL-PRF-55365 often does not match the observed behavior of tantalum polymer capacitors and (2) the statistical calculations behind the FRSP-90 tables create a testing disadvantage versus Weibull grading that is most keenly felt when there are no early failures during Weibull grading (the precise conditions under which use of the FRSP-90 tables is suggested).
Some of the disadvantage of the FRSP-90 tables comes from the assumption of constant failure rate versus the Weibull grading assumption of declining failure rate. This is primarily a disadvantage for MnO2-cathode capacitors. For tantalum polymer capacitors, the disadvantage is that the underlying statistics of FRSP-90 are least reliable when no failures occur, and many additional part hours are required just to satisfy the statistical confidence requirements.
A final concern is that both Weibull grading and the FRSP-90 alternative (when Weibull grading doesn’t work) are performed on parts that are not reflow-mounted on circuit boards. The concern here is that these methods provide no way to detect capacitors that are vulnerable to damage from the reflow mounting inevitably performed by the customer.
Industry experience in the commercial marketplace has demonstrated that some batches of tantalum capacitors (both MnO2-cathode and polymer-cathode) are vulnerable to damage from reflow mounting. So it is likely that some batches that are successfully Weibull graded to very high-reliability levels could be damaged by reflow mounting and then demonstrate lower reliability in the field than is implied by their Weibull grading level.
A vulnerability of this kind cannot be detected by Weibull grading since the graded capacitors cannot be both reflow mounted and shipped as new devices. For this reason, any alternative to Weibull grading should include reflow mounting of a sample of capacitors to demonstrate robustness against this threat.
Since the Weibull grading method doesn’t fit well with the time-to-failure behavior of tantalum polymer capacitors, it is reasonable to search for an alternative test method that allows assessment of reliability on a batch-by-batch basis (batch by-batch assessment is one of the real strengths of Weibull grading). Many alternatives exist among which there are three leading candidates.
One strategy is to return to the ER test method that employs non-accelerated life testing of many capacitors and could easily include reflow mounting. This method does away with concerns over inaccurate acceleration factors but requires large sample sizes and long periods of test time just to discover the failure rate of a limited number of batches. This methodology is trustworthy but highly impractical to implement on a batch-by-batch basis.
Another strategy is to adjust the requirements of MIL-PRF-55365 to allow voltages above 1.53Vr so that at least one failure will occur within the first 10 hours of testing. This strategy has the appeal of simplicity, but, as was seen previously for the 68uF, 16V tantalum polymer capacitors, grading under highly-accelerated test conditions can consume a substantial fraction of the useful life of the capacitors when the capacitors are not prone to early failures. If one were to choose this second strategy, it would also be well to consider employing a voltage acceleration formula better matched to tantalum polymer capacitors and to consider adding a test to assess sensitivity to reflow mounting.
A third strategy is to reflow-mount a disposable sample of capacitors and test them under accelerated conditions to validate the target failure rate. This third strategy would allow both voltage and temperature acceleration, employ acceleration formulas that are matched to the part type, and employ a practical accept/reject (A/R) ratio that allows for an occasional parts-per-million-level reflow failure without excessively inflating the part-hour requirements for a given failure rate level.
KEMET chose to pursue the third test strategy described above. The practical implementation of this strategy is as follows.
First, the test is considered a destructive test that is performed on a representative sample (usually 100 pieces) of reflowmounted capacitors. Unlike Weibull grading, the surviving tested samples are not shipped to customers, so there is no concern that significant useful life may be consumed during the accelerated test. Of concern is only that the A/R requirement is met at the end of the test to validate the desired low failure rate.
Second, both voltage and temperature are used as acceleration factors. The total acceleration sought is roughly a factor of 10,000 which is half of the maximum voltage acceleration allowed by MIL-PRF-55365. Acceleration formulas are employed that are matched to the specific part type to improve assessment accuracy. These acceleration formulas are based on the wearout mechanism, not mechanisms that cause premature failures. This adds a conservative bias to the testing since premature failures are generally more aggressively accelerated by a given test voltage than are wearout failures. This choice is made to assure that batches that do not have sufficient long-term life are detected and rejected, even when they do not generate early failures because they have uniform but sub-standard dielectric robustness.
Third, the objective of the test is to accumulate roughly 100,000,000 accelerated test hours with no more than 1 failure. Such performance demonstrates that the batch meets 0.001%/1000h observed constant failure rate (OCFR) which is equivalent to the Weibull D failure rate in MIL-PRF-55365. Either fewer accelerated test hours or less acceleration is required to achieve equivalence to Weibull failure rates C (0.01%/1000h) and B (0.1%/1000h).
The A/R ratio is set at 1/2 to accommodate the occasional parts-per-million-level failure that is expected due to the stresses of reflow mounting combined with the highly accelerated test conditions. An alternative to the A/R of 1/2 is to use an A/R ratio of 0/1 while allowing one retest. Again, the logic is to accommodate ppm-level reflow damage while rejecting systematically inferior batches.
Finally, the number of accelerated test hours used in this assessment is lower than would be required by the FRSP-90 tables. But we believe that the conservative testing bias introduced by using acceleration formulas based on the wear-out mechanism, rather than formulas based on premature failures, fully compensates for the reduced test hours.
It is one thing to create a new testing protocol when the existing test methods do not fit the devices being tested. It is quite another to successfully validate the new strategy in “the real world.” We were fortunate to have an opportunity to perform this validation during the course of responding to a customer’s problem.
This customer was building circuit boards that carried many thousands of MIL-PRF-55365 MnO2-cathode tantalum capacitors, all connected in parallel. Even though clusters of these capacitors were separately fused, when occasional failures occurred, the resulting “transient thermal event” during breakdown would cause non-repairable damage to the very expensive circuit board (see Fig. 4).

The customer believed that tantalum polymer capacitors would have the dual benefit of lower ESR and a more benign failure mode, and they were eager to give the capacitors a try. But they wanted assurance that the reliability of the tantalum polymer capacitors would be at least comparable to the “legacy” MnO2-cathode capacitors.
A relatively routine flow of mil-aerospace screening tests was defined for the tantalum polymer capacitors. This testing is similar to testing that MIL-PRF-55365 capacitors receive. On top of this routine testing, special KEMET screening was performed to select for shipment only the “best of the best” parts.
For the reasons detailed in this paper, we discouraged the customer from requiring MIL-PRF-55365 Weibull grading as part of the testing protocol. But they were adamant that they wanted parts that were known to be at least as reliable as the MIL-PRF-55365 Weibull D parts they were currently using. So, in place of Weibull grading, we suggested our new “Polymer Capacitor Reliability Assessment Test” (PCRAT) which follows the test strategy described above. PCRAT is performed on every batch. A majority of the batches pass the test, but occasional batches fail and are not shipped.
The first hurdle was cleared when these tantalum polymer capacitors passed the customer’s internal qualification testing program. Then the parts were introduced into high-volume manufacturing and were exposed to stringent production testing of the finished circuit boards.
Two significant findings came to light [1]: (1) the observed capacitor failures on production circuit boards dropped from 0.14% to only 0.01%, and (2) the few capacitors that did fail did not damage the circuit board which allowed rework (see comparison in Fig. 5) which provided significant cost savings. The end result is that the customer is very pleased with both the capacitors and the new reliability assessment method.

While MIL-PRF-55365 Weibull grading is an accepted and useful failure rate estimation tool for MnO2-cathode tantalum capacitors, it is not well suited for use with tantalum polymer capacitors which often are not prone to early failures. Because there are often no early failures when tantalum polymer capacitors are exposed to the allowed Weibull grading conditions, it is simply not possible to follow the procedure and perform the calculations for lack of the required time-to-failure data.
Another weakness of the MIL-PRF-55365 Weibull grading method is that the procedure is performed on unmounted capacitors. It is well known that some capacitors are more sensitive to the stresses of reflow mounting than others. This makes it possible for sensitive batches of capacitors to perform well during Weibull grading, but less well in the field after reflow mounting. It makes good sense to require reflow mounting prior to testing as part of any reliability assessment method that is chosen as an alternative to Weibull grading.
A new reliability assessment methodology is suggested in this paper. KEMET’s Polymer Capacitor Reliability Assessment Test (PCRAT) combines time-proven testing concepts from the old military Established Reliability programs with modern voltage and temperature acceleration techniques that are specially tailored to the parts under test. The balance among sample size, accelerated test conditions, test duration, and failure criteria is chosen to allow practical estimation of the mounted-part failure rate of tantalum polymer capacitors. And so far, customer experience with capacitors evaluated with this new test strategy is very good.
Erik Reed, VP Technical Fellow
Cristina Mota Caetano, Director Technical PM Ta BG